10. Advanced Plotting with matplotlib

Figures and main concepts from: realpython.com.

Learning Objectives

Be able to:

• Read a publically available file directly from google drive

• Use matplotlib’s advanced layout features for multiple plots

• Understand the difference between a “figure” and “axes” in matplotlib

Date files needed:

• california housing data (csv)

  • file id: 1lcMbOh19eUUhCdvSloNs5mOYLBCMkIgz

• county income data (xlsx)

  • file id: 1rmIPRkMAqqfY3TNpWZ13aV4PfuKihguM

Note

You can load data files directly from my google drive by using:
raw=pd.read_csv('https://drive.google.com/uc?id=FILE_ID')
where “FILE_ID” is the google drive file identifier given previously. Also, use either read_csv or read_excel as appropriate. For the california housing data, we would write:
raw=pd.read_csv('https://drive.google.com/uc?id=1lcMbOh19eUUhCdvSloNs5mOYLBCMkIgz')

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

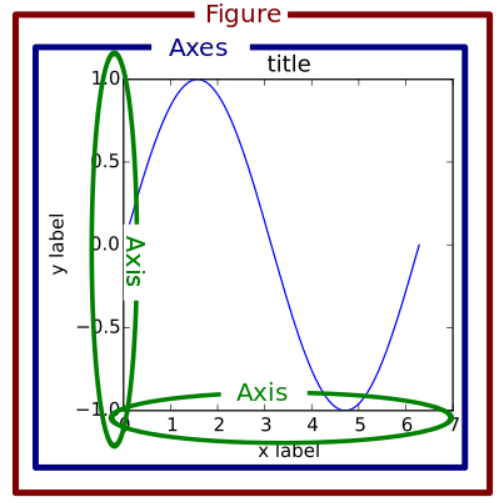
10.1. “Figure” versus “Axes” according to matplotlib

In matplotlib, a “figure” is the outer container that might contain multiple plots. The individual plots are referred to as “axes”. That is, we create a set of axes for every plot that we want. The plot itself can contain multiple curves by using multiple plt.plot() commands. In all of our previous lessons, we have only defined a single set of axes using for example fig, ax = plt.subplots(nrows=1, ncols=1)

Examples
fig, ax = plt.subplots(nrows=1, ncols=1) if we only have one axes (plot)
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2) if we define 2 axes in one figure with the axes named “ax1” and “ax2”.

Note

The names “fig”, “ax1”, “ax2” etc are up to you. There is nothing special about these particular names other than they are descriptive (easy to read) and short.

10.2. Creating rows and columns of axes

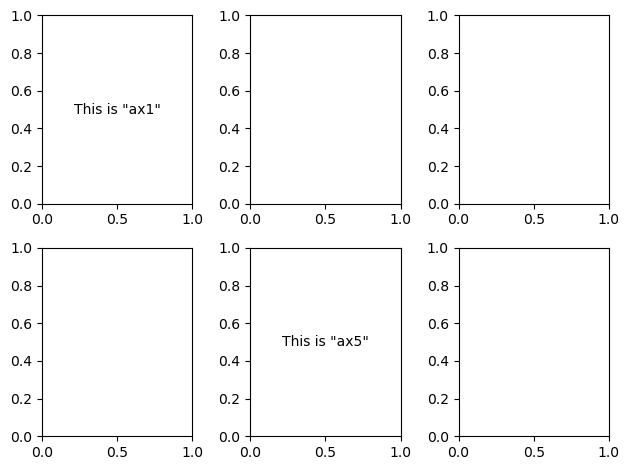
The command plt.subplots() creates a figure with the number of axes specified by the call. For example, plt.subplots(nrows=2, ncols=3) creates a figure with 6 sets of axes (2 rows by 3 columns) as shown below.

plt.subplots(nrows=2, ncols=3)
plt.show()

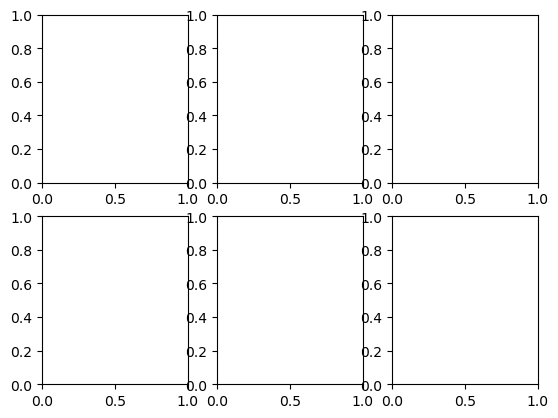
To make a plot within one of the axes, we need to access the axes by its name. We can do this by naming each axes. We usually call these ax1, ax2, etc. and specify them as a matrix. For example:
fig, ((ax1, ax2, ax3),(ax4,ax5,ax6))=plt.subplots(nrows=2, ncols=3)
fig, (ax1, ax2, ax3)=plt.subplots(nrows=1, ncols=3)
fig, (ax1, ax2, ax3)=plt.subplots(nrows=3, ncols=1)

fig, ((ax1, ax2, ax3),(ax4,ax5,ax6))=plt.subplots(nrows=2, ncols=3)
ax1.annotate('This is "ax1"',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
ax5.annotate('This is "ax5"',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
fig.tight_layout() # this removes the overlap that we had above
plt.show()

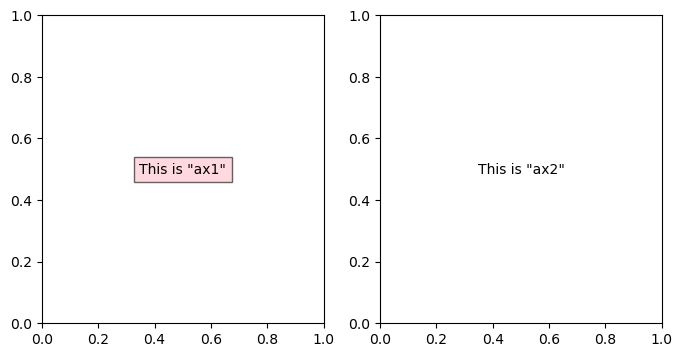
And for 2 axes in a row:

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2,figsize=(8, 4))
ax1.annotate('This is "ax1"',(0.5,0.5), xycoords='axes fraction', va='center', ha='center', bbox=dict(facecolor='pink', alpha=0.6),fontsize=10)
ax2.annotate('This is "ax2"',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
plt.show()

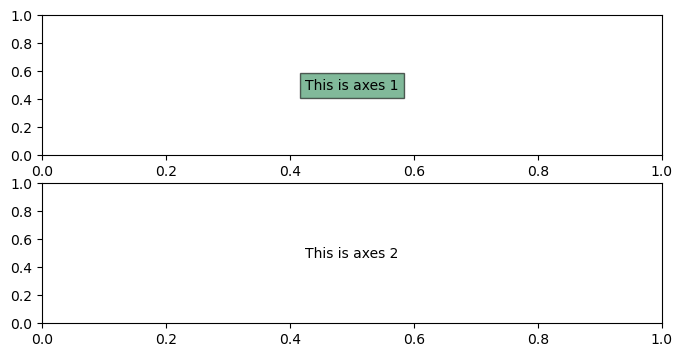
or for 2 axes in a column:

fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1,figsize=(8, 4))
ax1.annotate('This is axes 1',(0.5,0.5), xycoords='axes fraction', va='center', ha='center', bbox=dict(facecolor='seagreen', alpha=0.6),fontsize=10)
ax2.annotate('This is axes 2',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
plt.show()

10.3. Adding data to our axes

Now let’s add some data to our axes and perhaps different plot types. First, let’s generate some data to plot

x = np.random.randint(low=1, high=11, size=50) #generate 50 random integers between 1 and 10
y = x + np.random.randint(1, 5, size=x.size)  #generate 50 random integers between 1 and 4 and add to x
data = np.column_stack((x, y))
data[0:5] #with numpy arrays we use different notation to slice elements as compared to pandas

array([[ 1,  2],
       [ 6,  7],
       [ 5,  7],
       [ 8, 11],
       [10, 13]])

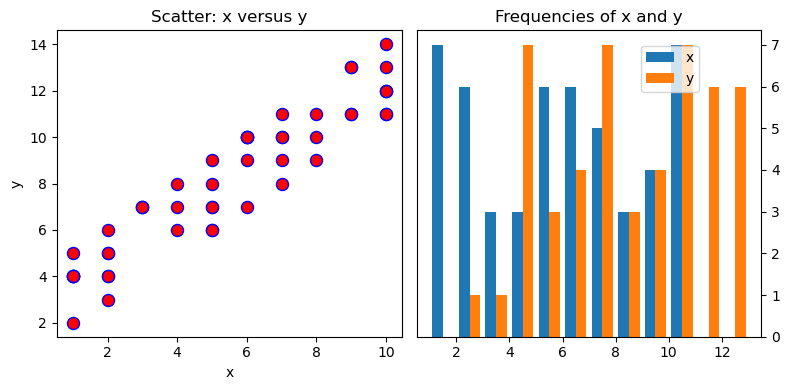
Now we will add a few options and make some nice plots.

# create a figure with two axes in a row and adjust the overall figure size
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2,figsize=(8, 4))
# make a scatter plot in the first axes (ax1)  
# marker = circle, color = red, edgecolor = blue, size=75 points
ax1.scatter(x=x, y=y, marker='o', c='r', edgecolor='b', s=75)
ax1.set_title('Scatter: x versus y') # add title to ax1
ax1.set_xlabel('x') # add xlabel to ax1
ax1.set_ylabel('y') # add ylabel to ax1

# now let's work on the second axes (ax2)
ax2.hist(data, bins=np.arange(data.min(), data.max()),label=('x', 'y')) #define a histogram
ax2.legend(loc=(0.65, 0.8)) #by using "label" in hist() we can now show a legend, location at 65% in horizontal and 80% in vertical direction
ax2.set_title('Frequencies of x and y') # add title to ax2
ax2.yaxis.tick_right() # place the y-axis ticks on the right side rather than left

fig.tight_layout() # keep axes tight together but avoid overlap

10.4. More advanced layouts (span rows and/or columns)

If you need more advanced layout beyond simple grids of graphs, then Matplotlib’s gridspec module allows for more subplot customization. Pyplot’s subplot2grid() interacts with this module.

Say we want this setup:

Set it up like a 3 row x 2 column grid (as shown below) then allow ax1 to span 2 columns and 2 rows:
Notice below the numbering of the grid. The upper left plot is at location (0,0) and the lower right would be (2,1).

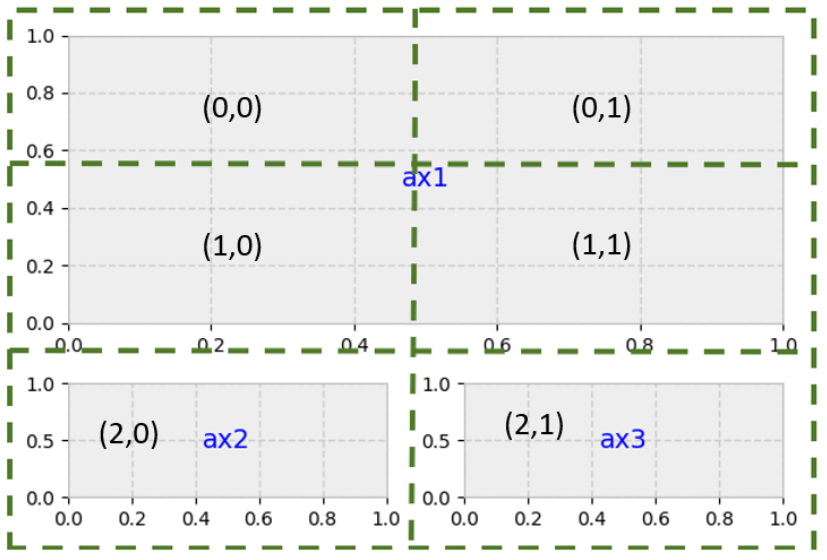
gridsize = (3, 2) # 3 rows x 2 columns
fig = plt.figure(figsize=(12, 8)) #overall size of figure contains total grid 3x2
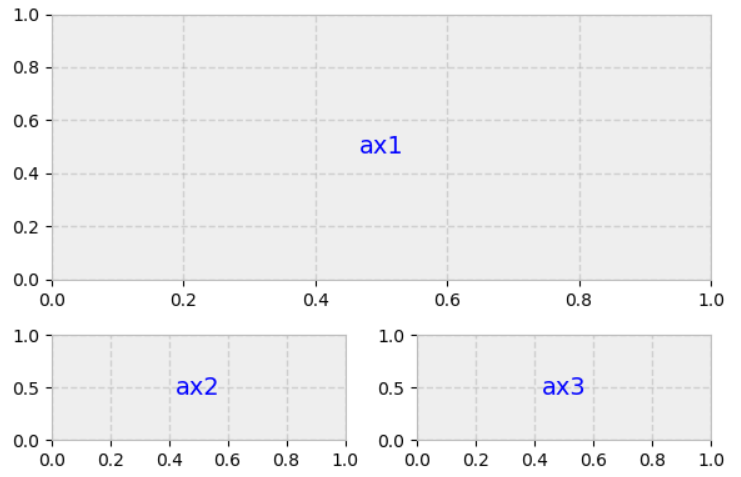
ax1 = plt.subplot2grid(gridsize, (0, 0), colspan=2, rowspan=2) # start at axes (0,0) and span 2 col and 2 rows
ax2 = plt.subplot2grid(gridsize, (2, 0)) #3rd row, 1st col
ax3 = plt.subplot2grid(gridsize, (2, 1)) #3rd row, 2nd col
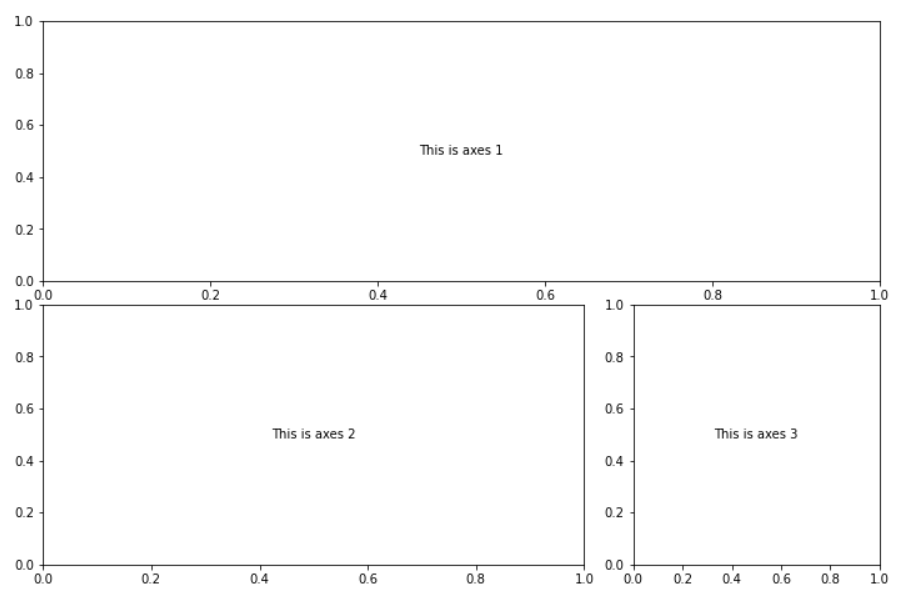
ax1.annotate('This is axes 1',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
ax2.annotate('This is axes 2',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
ax3.annotate('This is axes 3',(0.5,0.5), xycoords='axes fraction', va='center', ha='center')
plt.show()

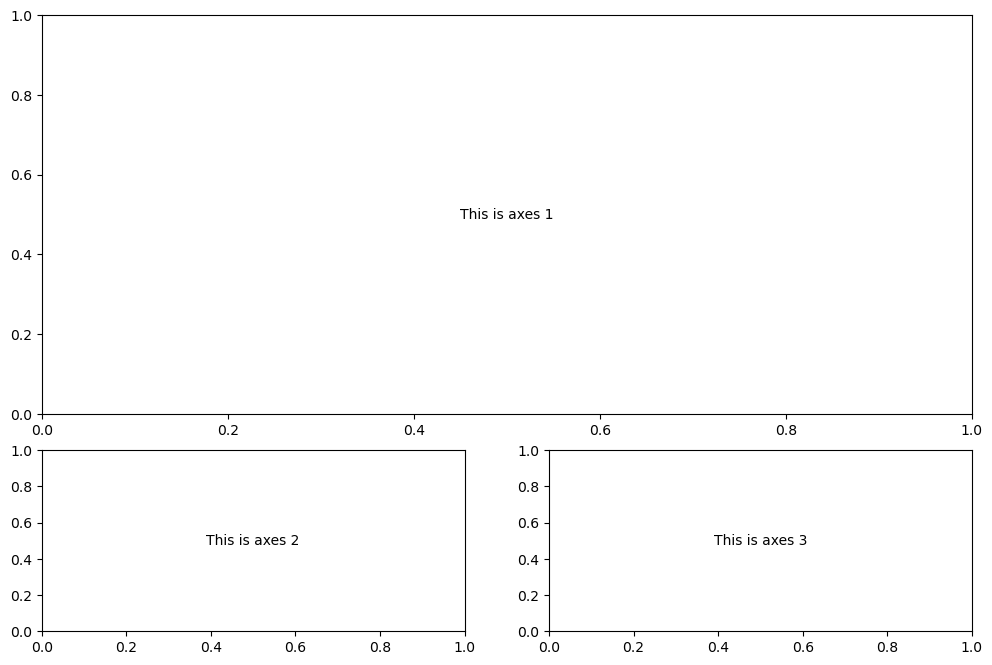
You could make many creative layouts using the simple concepts shown in the previous output.

10.5. Example 1 California housing data

Let’s take a look at some California housing data whose description can be found at https://developers.google.com/machine-learning/crash-course/california-housing-data-description

raw2=pd.read_csv('https://drive.google.com/uc?id=1lcMbOh19eUUhCdvSloNs5mOYLBCMkIgz')

housing=raw2.copy()
housing

	longitude	latitude	housing median age	total rooms	total bedrooms	population	households	median income (10k)	median house value
0	-122.23	37.88	41	880	129	322	126	8.3252	452600
1	-122.22	37.86	21	7099	1106	2401	1138	8.3014	358500
2	-122.24	37.85	52	1467	190	496	177	7.2574	352100
3	-122.25	37.85	52	1274	235	558	219	5.6431	341300
4	-122.25	37.85	52	1627	280	565	259	3.8462	342200
...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25	1665	374	845	330	1.5603	78100
20636	-121.21	39.49	18	697	150	356	114	2.5568	77100
20637	-121.22	39.43	17	2254	485	1007	433	1.7000	92300
20638	-121.32	39.43	18	1860	409	741	349	1.8672	84700
20639	-121.24	39.37	16	2785	616	1387	530	2.3886	89400

20640 rows × 9 columns

y = housing.iloc[:, -1] #home price
pop=housing.loc[:, 'population'] #population
age=housing.loc[:, 'housing median age'] #average age of home

#create layout
gridsize = (3, 2)
fig = plt.figure(figsize=(8, 7)) #overall size of figure
ax1 = plt.subplot2grid(gridsize, (0, 0), colspan=2, rowspan=2)
ax2 = plt.subplot2grid(gridsize, (2, 0))
ax3 = plt.subplot2grid(gridsize, (2, 1))

#fill layout with plots
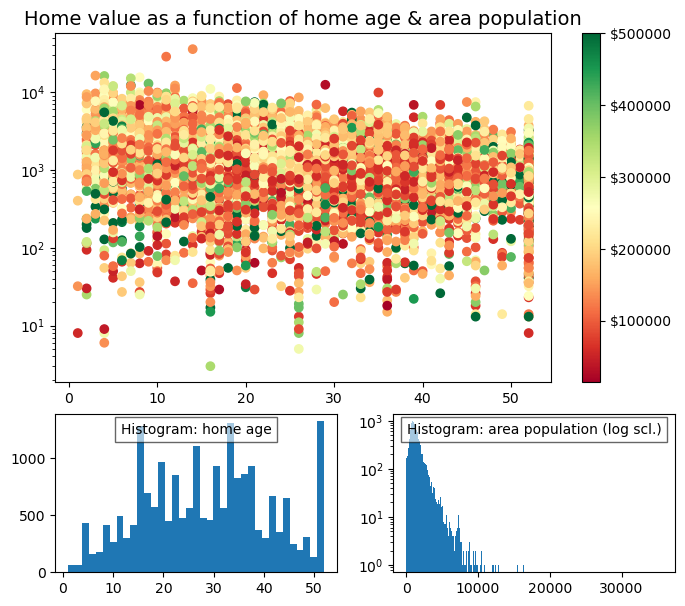
ax1.set_title('Home value as a function of home age & area population',fontsize=14)
sctr = ax1.scatter(x=age, y=pop, c=y, cmap='RdYlGn')
plt.colorbar(sctr, ax=ax1, format='$%d')
ax1.set_yscale('log')
ax2.hist(age, bins='auto')
ax3.hist(pop, bins='auto', log=True)

ax2.annotate('Histogram: home age',(0.5,0.9), xycoords='axes fraction', va='center', ha='center', bbox=dict(facecolor='white', alpha=0.6),fontsize=10) 

ax3.annotate('Histogram: area population (log scl.)',(0.5,0.9), xycoords='axes fraction', va='center', ha='center', bbox=dict(facecolor='white', alpha=0.6),fontsize=10) 


plt.show()

10.6. Example 2 County income data

raw=pd.read_excel('https://drive.google.com/uc?id=1rmIPRkMAqqfY3TNpWZ13aV4PfuKihguM')
data=raw.copy()
data.columns=['county', 'state', 'households',
       '<10k',
       '10k_15k',
       '15k_25k',
       '25k_35k',
       '35k_50k',
       '50k_75k',
       '75k_100k']
data

	county	state	households	<10k	10k_15k	15k_25k	25k_35k	35k_50k	50k_75k	75k_100k
0	Autauga	Alabama	21397	1417	1172	2219	1684	2721	3817	2931
1	Baldwin	Alabama	80930	4068	3685	7092	8403	11245	14928	10374
2	Barbour	Alabama	9345	1391	796	1641	1092	1331	1239	769
3	Bibb	Alabama	6891	570	554	897	610	1021	1100	1119
4	Blount	Alabama	20847	1706	1145	2199	2600	2921	4050	2497
...	...	...	...	...	...	...	...	...	...	...
4925	Sweetwater	Wyoming	15523	805	645	1202	868	1653	2605	2506
4926	Teton	Wyoming	9019	182	198	667	383	838	1552	1448
4927	Uinta	Wyoming	7597	382	232	559	791	934	1451	1241
4928	Washakie	Wyoming	3365	144	174	286	379	541	710	519
4929	Weston	Wyoming	2891	181	143	338	246	398	433	433

4930 rows × 10 columns

The above data shows the total number of households in each county of each state and a breakdown of the number of households that have an income in one of the indicated ranges.

For example, 2931 households have an income between 75,000 and 100,000 in Autauga County, Alabama. This represents 2931/21397*100 = 13.7% of all households in Autauga County.

10.7. Exercises

10.7.1. Problem 1

Complete the following steps on the county income data:

First, you need to fix the data set to remove duplicates using drop_duplicates(). Instead of 4930 rows you should get 3142 records.

Determine the following:

1. The number of households that have an income greater than 100,000 for each county across the USA. Add this data to the dataframe.

2. The percentage of households for each income range for each county, i.e. divide the data for each row by “households” and multiply by 100.

10.7.2. Problem 2

Using the cleaned data from Problem 1, plot the following in the layout described below.

1. The percentage of households with an income less than 50,000 and the percentage of households with an income greater than 100,000 for every state in the US.

2. The same data but now for every county in Virginia.

3. A bar chart for the same data but now for Montgomery County, Virginia.

The three plots should be laid out similar to the figure below where each plot is the same height but plot 1 has a width of 3, plot 2 has a width of 2 and plot 3 has a width of 1.